I thought I’d write something up to be a little more fundamentally educational rather than making guesses on market or stock directions. There is a lot of excitement recently regarding 0DTE (zero days to expiration) options. I don’t intend for this to be an all encompassing educational post, just a general walkthrough of how Options are priced, how they move, and why these particular types of options are so attractive in this trading environment.
What Is An Option?
An Option is a Derivative contract, meaning its value is based on an underlying security. The 2 key features of a contract are its strike price and an expiration date. A Call Option gives the contract owner the right to buy the underlying security at the strike price. A Put Option is the opposite in that the owner of the contract has the right to sell the underlying security at the strike.
Note: For purposes of this post I’ll stick with Calls as Puts are just the flipside of Calls.
How Are Options Priced?
There are two parts of the value of an Options contract. The first is called Intrinsic Value, which is simply the difference between the strike price and the current price. If the strike is “In the Money”, then that intrinsic value would be reflected as part of the option price. For example, if a call has a $100 strike and the underlying stock is $105, then the option contract has a $5 intrinsic value.
The other part of the options price is related to a set of other variables related to the underlying stock price and movements. They are represented by several Greek letters:
1- Delta: Change in the Option Price with every dollar change in the underlying security. E.g., If the option has a Delta of 0.2 then the Call price will increase by 20 cents when the Underlying Stock moves $1.
2- Gamma: Change in the Option Delta with every dollar change in the underlying security. E.g., if the option has a Gamma of 0.05 then the Delta will increase by .05 when the Underlying Stock moves $1.
3- Theta: Change in the Option Price with every day that passes.
4- Rho: Sensitivity of Options price with relation to change in the risk-free rate environment. (I won’t go into this is certainly a more advanced aspect of options pricing which I am not that familiar, but noting it here to be thorough).
5- Vega: (Not a true Greek Letter, just a made-up word, but whatever). Change in price due to increase in implied volatility. (I also won’t be going into this as I have little experience/familiarity with this).
I won’t go into specifics, but each of these is utilized in the Black-Scholes formula of Options Pricing (this formula is used to generate a theoretical price for an option and is sometimes used in models for arbitrage purposes. The specifics of this are way beyond the scope of this post but, again, noting for thoroughness). Delta is certainly an important one to watch as this is a direct representation of the change in the option as the underlying stock changes.
Gamma is second most in-focus variable as this directly affects the Delta and, thus, the Options Price. Theta is the most interesting to me as it doesn’t change with relation to any moves in the underlying security. Instead, it changes with relation to the expiration date of the contract. While other variable contributes something important to the option price, Theta may be one of the most important as it is simply time decay of the value of the options contract.
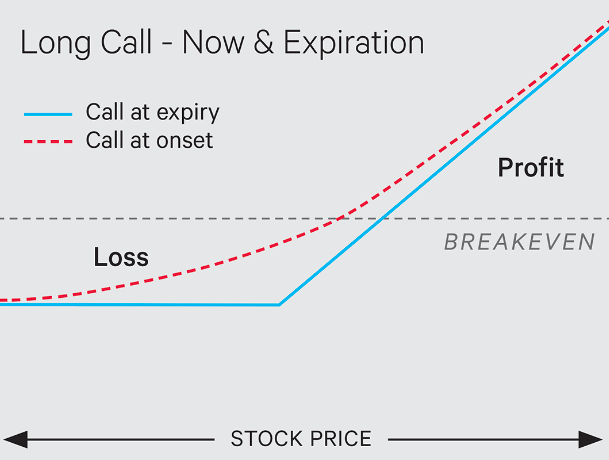
I borrowed this snapshot from here: Risk Profile Tool: The Option Trader’s Travel Companion – Ticker Tape (tdameritrade.com). I wanted to post this snapshot as an example of the difference the time value makes on the profitability potential on an Option trade (This article goes through in more detail). The main idea is that when there is lots of time value on an option, the cost of the option is inflated with a premium on top of its intrinsic value. However, as the option gets closer to expiration, the risk profile is much more rigid and straightforward. This is because the other Greek variables no longer have any impact on the options price. All that is left is the intrinsic value.

The benefits of long-dated options lie in the fact that they simply have lots of time before they expire. The theta curve is relatively flat, though still decreasing, when there is lots of time. So the real movement in the option price is simply related to the movement of the underlying stock. And if it really moves against you, then the high amount of time value should still provide some money left over in the option value (consider this a consolation prize).
On the flipside is options pricing at expiration. This brings us to what we have been seeing and hearing about so much in the past year: 0DTE options. In the past, options were offered usually on a monthly basis, so the pricing and trading of options had much bigger implications for options traders as the decisions in their trading had to consider the premiums associated with the contracts. However, with 0DTE options, this essentially removes the theta portion of the options price and the option therefore becomes a lottery ticket.
Once the option expires, the matter of intrinsic value is fairly binary in that it is either worth something or it is not. Traders (in this case, I’d say the majority are more like gamblers) may take advantage of 0DTE options by placing their wagers on out of the money options for cheap. They are cheap because their intrinsic value at the time would be $0 (hence “out of the money”) and their theta value is near 0 because it is already expiration day. So they can load up in either direction for 10 times what they might be able to afford of the actual underlying stock and rake in the profits if it goes their way.
So this is just an overview of the basics of how options move. I thought it would be a good refresher for anyone who may be interested in how they function or for anyone without any prior knowledge of them. There is a lot (a LOT) more to trading options to consider before diving in. I recommend reading a few books to better understand basic strategies and risks with these. As for 0DTE, what can I say? If you are good at picking direction then they may provide better payout odds than the casino. Otherwise, hit the Blackjack tables.

