Looking back at an optimal put hedge on GLD
In Tim's after the close wrap-up video Thursday ("Fire, Walk With Me"), he noted how precious metals had fallen out of bed recently. Below is a look at what happened with an optimal put hedge on the gold-tracking ETF GLD Thursday. Then, a preview of an idea for timing when to roll options. First, though, a quick reminder about optimal puts.
About Optimal Puts
Optimal puts are the ones that will give you the level of protection you want at the lowest possible cost. Portfolio Armor (available on the web and as an Apple iOS app), uses an algorithm developed by a finance Ph.D to sort through and analyze all of the available puts for your stocks and ETFs, scanning for the optimal ones.
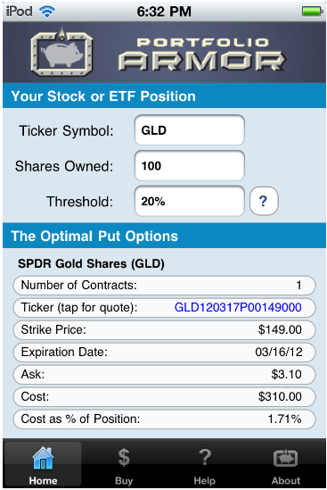
An optimal put hedge on GLD
Here are the optimal puts we pulled up on GLD in a hedging update earlier this month. These were the optimal puts on September 9th to hedge against a greater-than-20% drop in GLD over the next six months:
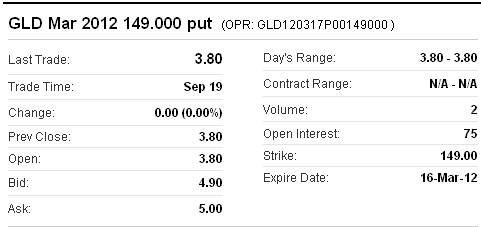
Those GLD puts on Thursday
They didn't trade on Thursday, but note the bid-ask on them in the quote below: $4.90 by $5.00. In the screen cap above, the ask on them was $3.10.
Timing when to roll options
In a previous post I mentioned that a quant on the Portfolio Armor team was starting a post doctoral fellowship this fall. I had asked him recently for a rule of thumb about the best time to roll options before time decay accelerates. He said he'd check the academic finance literature on it. He e-mailed me Thursday saying he hadn't found anything in the literature about that, but he'd had an epiphany about it. The details still need to be worked out, but I thought it was interesting enough that I'd share the the idea here. This is from his e-mail:
As you know, the time decay is given by the Greek "theta"… the problem is that to compute an option's theta you need a model (Black-Scholes, or some alternative), which goes against the whole premise of Portfolio Armor: it is model-free and relies on no parametric assumptions [so there's no chance of model errors].
Here he notes that you don't need a model to figure out the time value on an option:
We can figure out the time value on any option without a model: it is the difference between the market price and the intrinsic value, where the latter is Max{(S-K),0} for calls and Max{(K-S),0} for puts.
And then here's his epiphany to use a little calculus to time the roll of the options before theta burn kicks in:
We can look at the discrete-time differential (approximation of the first derivative) of the time-value component and try to find the point before time-decay is accelerated (the second derivative), say, starting three to four weeks before expiration. Once that trigger is hit, you can start emailing out reminders to users that they may want to roll their protection. I can work on this more and try to come up with a more formal algorithm, which can be included in the next version of Portfolio Armor, if you would like.
I thought it was interesting to see how a quant's mind works when tackling a problem like this.
Disclosure: I am long puts on GLD.