“Patience is waiting. Not passively waiting. That is laziness. But to keep going when the going is hard and slow – that is patience.” ~ Unknown
Probabilities
Let’s now discuss what a probability distribution is.
A probability distribution is defined in terms of being an underlying sample space which is the set of all possible outcomes of the random phenomenon being observed.
Let’s take an example. When you sit down to play blackjack, there are a discrete number of possible hands.
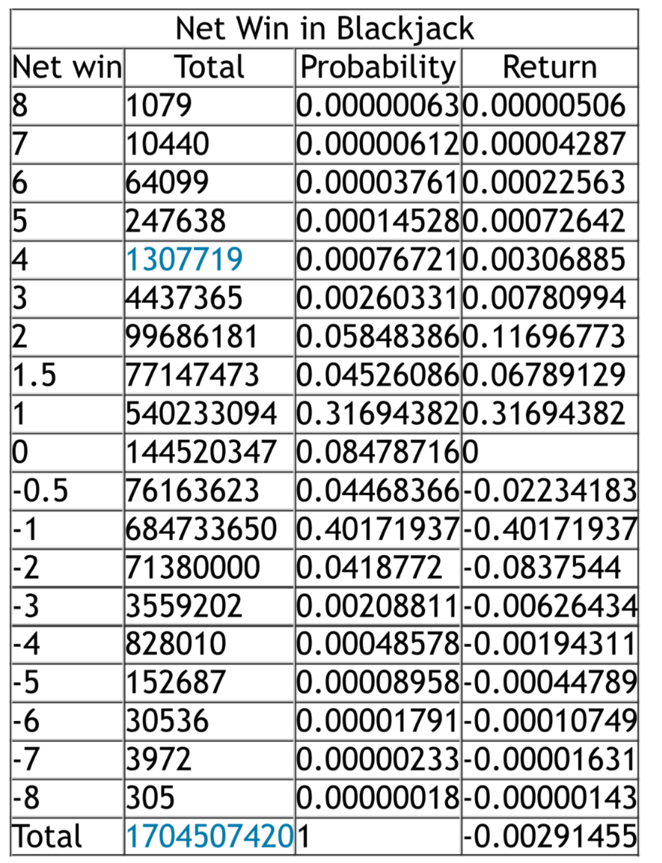
Over time, you will usually win one betting unit or lose one unit to the dealer. Sometimes you might win blackjack, which pays 2:1. There are also splits and double down events which change the number of bets won or lost. Overall there are 1.7 billion possible combinations of events, with average loss of about 0.003 units per hand on average to the dealer.
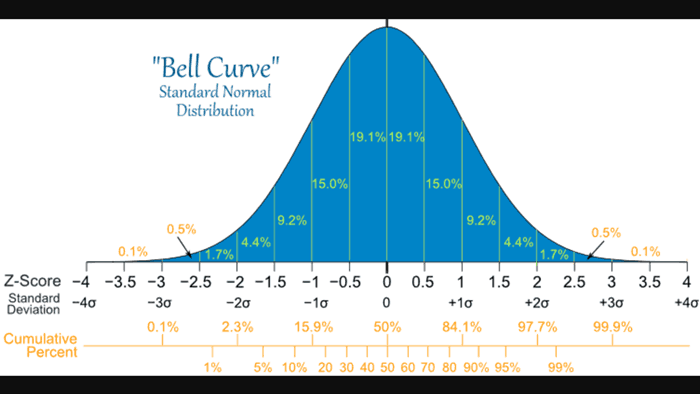
Focus on the second column. If you flip the image 90 degrees and look at the total number of events, you can see a distribution curve form- rare events at the ends and common events at the center. Mathematicians design formulas which approximate these distributions. One of these is the *normal* distribution, or the infamous bell curve.
Standard deviation means roughly the approximate average difference of the average value in a set of numbers and one value in the same set. In the normal distribution, one standard deviation above the mean is 34% above the mean and one standard deviation below the mean is 34% below the mean. The middle part of 1 standard deviation comprises the middle 68% of values. 2 standard deviations are 95% of values. This is approximately considered “significant” in the biomedical sciences and the boundaries of “normal” and “abnormal” in medical testing.
Using the normal distribution, and the famous Black Scholes equation, we can estimate the probability of an option being a certain value at a certain time.
In addition the risk:reward ratio in options is scaled roughly to the inverse of the probability of being profitable. Options are thus theoretically zero-sum.
Or are they? These are approximations. Since Black Scholes is how market makers set up markets and communicate with one another this is what we are “supposed to” use. Knowing how the real market deviates from the normal distribution is critically important in taking advantage of option trading.
We will discuss paths around zero sum later.